RWA#1:Unit M Concepts 4-6: Graphing and Identifying all Parts of an Ellipse

1) Definition
"The set of all points such that the sum of the distance from two                   points is a constant." (Crystal Kirch) 

2)

http://www.mesacc.edu/~marfv02121/readings/conics/conics-2.GIF

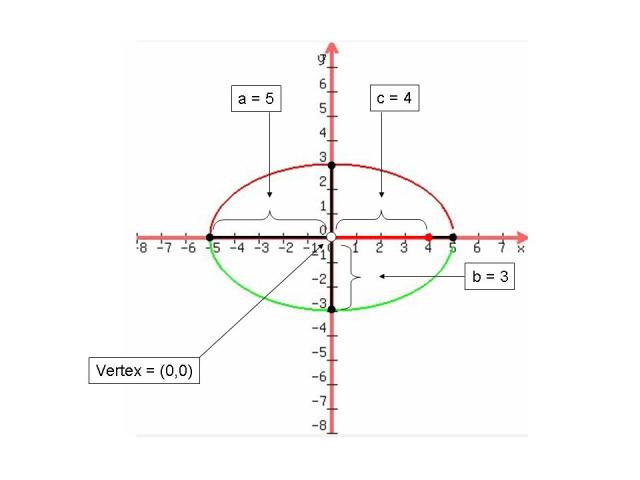
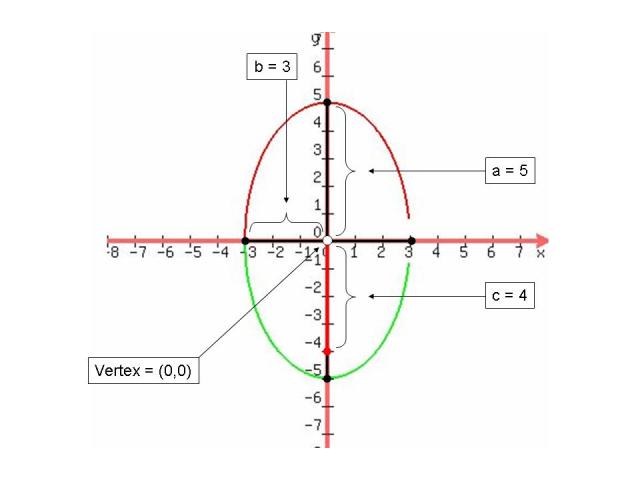
      The above equations show an ellipse in standard form also meaning both term terms are squared, added, and have different coefficients. In standard from we can find the vertex, by using the h and k, and we can find our a and b by taking the square root of the a and b in the standard form. a is the distance in units away from the center and the vertex and b is the distance in units from the center to the co vertices. you can also use b to find the co-vertices which are the endpoints of the minor axis. To find c you must use the equation a^2 -b^2=c^2. c is the distance in units from the center to the foci. the c will also be a part of the foci. The below pictures give a visual. 
     

Horizontal 

http://theo.x10hosting.com/examples/Ellipse/Ellipse6.jpg

Vertical 

http://theo.x10hosting.com/examples/Ellipse/Ellipse7.jpg

     The following parts to graph an ellipse are the:  foci's, major axis, minor axis, and the eccentricity. The foci are spaced equally on each side of the center and they always lies on the major axis.The closer the foci is from the end point the skinnier the graph gets. To graph the foci you must plot the amount of c units to the right/left if x is squared but if y is squared then plot them up/down. identify whether the major axis is horizontal or vertical you must see if the bigger denominator in under the "y" squared or the "x" squared. If it is the bigger denominator is under the "x" squared term than it is horizontal and if its under the "y" squared term than it is vertical. The eccentricity of an ellipse (the measurement of how much a conic section varies from being a circle and for must be) must be greater than 0 but less than one. To find it you divide c and a. For more detailed instructions see:  http://jwilson.coe.uga.edu/EMAT6680/Brown/6690/InstrUnit/DayFive.htm

For better instructions on how to graph an ellipse watch the video below.

3) Real World Application 

Our solar system is an example of an ellipse. You may think that most objects in space orbit in circles, however that is not the case. Although some do follow circular orbits most orbits are shaped like a stretched out circle. All of the planets in our solar system move along elliptical orbits having the sun as a foci. The orbits of the moon and satellites of the moon are also elliptical. (http://www.windows2universe.org/physical_science/physics/mechanics/orbit/ellipse.html)

4) Works cited

•  http://www.mesacc.edu/~marfv02121/readings/conics/conics
• 2.GIFhttp://theo.x10hosting.com/examples/Ellipse/Ellipse6.jpg 
• http://theo.x10hosting.com/examples/Ellipse/Ellipse7.jpg
• https://www.youtube.com/watch?v=5nxT6LQhXLM
• http://www.windows2universe.org/physical_science/physics/mechanics/orbit/ellipse.html
• http://jwilson.coe.uga.edu/EMAT6680/Brown/6690/InstrUnit/DayFive.htm