The difference quotient, which is shown in the link below, comes from the slope of the secant line through two points on the graph of f. These are the points with x-coordinates x and x + h. The difference quotient is used in the definition the derivative. The difference quotient allows you to find the slope of any curve or line at any single point. The difference quotient is the change in "y" divided by the change in "x." The only difference is that in the slope formula, y is used as the y-axis, but in the difference quotient, the change in the y-axis is described by f(x).
Thursday, June 5, 2014
Wednesday, June 4, 2014
WPP#13-14: Unit P concept 6-7: Applications with Law of Sines and Cosines
1.) Ricky and Ana went a a family bbq to watch the game. However, no one could find the remote to turn on the tv so they quickly all tried to look for it before the game started. Ana looked under the couch when it was north of the couch and at Ricky was looking in the cabinets which was 25 yards away from Ana found it. Ricky saw the remote N28E from a north-south line through where was standing and Ana saw the ball's path N39W from a north-south line through where she is standing. What is the distance between Amarie and the football?
2) Ricky and Ana were playing baseball and they both ran to catch the ball. Ricky ran 12 yards at a bearing on 56 degrees and Ana ran 14 yards at a bearing of 315 degrees. how far apart were they before starting to run?
2) Ricky and Ana were playing baseball and they both ran to catch the ball. Ricky ran 12 yards at a bearing on 56 degrees and Ana ran 14 yards at a bearing of 315 degrees. how far apart were they before starting to run?
Monday, May 19, 2014
BQ#6: Unit U
1. What is a continuity? What is a discontinuity?
A continuity is a predictable graph in which you can draw without lifting your pencil and does not have jumps, breaks, or holes. To see an example of a continuous graph look at the first image below. A discontinuity on the other hand consists of non removable and removable. A non removable is non removable for the fact that there are different left and right heights on both sides of the graph, the graph is oscillating meaning it is extremely wiggly, or there is an unbounded behavior meaning that there is a vertical asymptote. At vertical asymptote keeps going and going closer and closer to the graph. When saying there are different left and rights, it simply means that if you put your hand on the left side and the right side of the graph and slide them together, they do not meet. A removable discontinuity is a point discontinuity meaning that there is a hole in the graph, as seen in the second image below.
 |
| http://www.analyzemath.com/calculus/continuity/continuous_1.gif |
 |
| https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcTfGXTPwPhR-q7-0XVjAsFKgDYLVYvmiIoGlO2I_UFAHoiBrlgl |
2. What is a limit? What is a discontinuity?
A limit is the intended height of a function, meaning its where two graphs are to meet up with each other. It is not able to exist when there is an unbounded behavior meaning there is a vertical asymptote, it is oscillating, and there are different left and right heights. An example of each is shown below.
Unbounded behavior

http://shell.cas.usf.edu/~ssuen/2233.2013s/c/chapter1.diagrams/1.6.18.png
Different left and right

http://image.tutorvista.com/content/feed/u364/discontin.GIF
Oscillating

http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit-graph8.jpg
3. How do we evaluate limits numerically, graphically, and algebraically?
Numerically means to set up a table. You are to have the limit in the middle and three boxes on each side. On far right side box you add 1/10 and the far left you subtract 1/10. From each sides you are to see clearly that the numbers keep getting a little closer and closer. To see an example look below. To evaluate a limit graphically you simply put a hand on the left and right side of the graph and slide them together. To evaluate it algebraically you may use substitution, which is simply plugging in the x value and solving. nalizing/conjugate method which is multiplying the conjugate and canceling. A conjugate is taking the radical expression and changing its sign.
Works Cited
http://www.analyzemath.com/calculus/continuity/continuous_1.gif
https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcTfGXTPwPhR-q7-0XVjAsFKgDYLVYvmiIoGlO2I_UFAHoiBrlgl
http://shell.cas.usf.edu/~ssuen/2233.2013s/c/chapter1.diagrams/1.6.18.png
http://image.tutorvista.com/content/feed/u364/discontin.GIF
http://webpages.charter.net/mwhitneyshhs/calculus/limits/limit-graph8.jpg
Wednesday, April 16, 2014
BQ#2: Uit T Concept Intro
The trig functions when graphed relate to the unit circle because when their values graphed and on the unit circle are the same there simple extended when there graphed.
Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?
It takes up to all four quadrants to repeat the same pattern. tangent and cotangent have a period of pi because they already have a positive and negative value on the first two quadrants.
Sine and cosine can not be bigger than one because of their ratios.
Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?
It takes up to all four quadrants to repeat the same pattern. tangent and cotangent have a period of pi because they already have a positive and negative value on the first two quadrants.
Sine and cosine can not be bigger than one because of their ratios.
Friday, April 4, 2014
Reflection#1: Unit Q Concept 5: Verifying Trig Identities
1. What does it actually mean to verify a trig function?
It means to solve each side of the equation so that they are equal to each other. You are proving that the identity is always true.You must simplify one of the sides by finding the GCF, substitution for an identity, multiplying by the conjugate, combining fractions with a binomial denominator, separating fractions with monomial denominators, or factoring as you break things down.The zero product property (ZPP) may apply which means your equation is equal to zero.
2. What tips and tricks have you found helpful?
The process of verifying trig functions a bit quicker when having the identities memorized so that you won't have to keep looking back and checking what they are. Another way to make things a bit easier is to be fully aware of what you are able to do with the trig functions such as, substituting an identity, multiplying by the conjugate, separating fractions with monomial denominators etc.Always try something even if you think your unsure of what to do. Once you start the problem you start to notice things that you can either cancel, substitute, factor etc.RRemember that you can never divide by a trig function.
3. Explain your thought process and steps you take in verifying a trig function. Do not use a specific example but speak in general terms in what you do no matter what they would live you.
It is better to first work with the one side of the equation that is more complicated and then you can move onto the other. You must look if there is a GCF, substitution for an identity, you are able to multiply by the conjugate, combine fractions with a binomial denominator, separate fractions with monomial denominators, or factor. In order to fully solve you must continue to look for these opportunities. Keep in mind that you may convert some terms to sines and cosines but not all. You cannot touch the right side.There is not only a one way process however it is possible.
It means to solve each side of the equation so that they are equal to each other. You are proving that the identity is always true.You must simplify one of the sides by finding the GCF, substitution for an identity, multiplying by the conjugate, combining fractions with a binomial denominator, separating fractions with monomial denominators, or factoring as you break things down.The zero product property (ZPP) may apply which means your equation is equal to zero.
2. What tips and tricks have you found helpful?
The process of verifying trig functions a bit quicker when having the identities memorized so that you won't have to keep looking back and checking what they are. Another way to make things a bit easier is to be fully aware of what you are able to do with the trig functions such as, substituting an identity, multiplying by the conjugate, separating fractions with monomial denominators etc.Always try something even if you think your unsure of what to do. Once you start the problem you start to notice things that you can either cancel, substitute, factor etc.RRemember that you can never divide by a trig function.
3. Explain your thought process and steps you take in verifying a trig function. Do not use a specific example but speak in general terms in what you do no matter what they would live you.
It is better to first work with the one side of the equation that is more complicated and then you can move onto the other. You must look if there is a GCF, substitution for an identity, you are able to multiply by the conjugate, combine fractions with a binomial denominator, separate fractions with monomial denominators, or factor. In order to fully solve you must continue to look for these opportunities. Keep in mind that you may convert some terms to sines and cosines but not all. You cannot touch the right side.There is not only a one way process however it is possible.
Tuesday, April 1, 2014
SP#7: Unit Q Concept 2: Find all trig Functions when given one trig function and quadrant
This Blog Post was made in collabortion with Ismael. Check out his awesome blogposts here
Wednesday, March 26, 2014
I/D#3: Unit Q: Pythagoreom Identities
Inquiry Activity Summary:
1.Sin2x+cos2x=1 comes from the identity, Pythagorean theorem, which is a factor or formula that is proven.The Pythagorean theorem, a^2+b^2=c^2 is replaced x^2+y^2=r^2 because of the fact that they hold the same values.
2. To derive the two remaining Pythagorean Identities from sin2x+cos2x=1 you must first, divide everything by r^2 and after doing that we get x^2/r^2+y^2/r^2=1. You can then notice that they x/ r is cosine and y/ r is sine meaning that you can put sin2x+cos2x=1 in place.
Inquiry Activity Reflection:
1. The connections that I see between Unit N,O,P, and Q so far are all related to the unit circle. In order to solve and understand most of them, you must fully understand and keep in mind the unit circle. Having memorized the unit circle is key.
2. If i had to describe trigonometry in THREE words, they would be difficult, challenging, and memorization. Trigonometry really requires a lot of practice and memorization of the unit circle. You can not solve the problems if you do not know the unit circle, formulas, sin, cos, tan, and so much more.
1.Sin2x+cos2x=1 comes from the identity, Pythagorean theorem, which is a factor or formula that is proven.The Pythagorean theorem, a^2+b^2=c^2 is replaced x^2+y^2=r^2 because of the fact that they hold the same values.
2. To derive the two remaining Pythagorean Identities from sin2x+cos2x=1 you must first, divide everything by r^2 and after doing that we get x^2/r^2+y^2/r^2=1. You can then notice that they x/ r is cosine and y/ r is sine meaning that you can put sin2x+cos2x=1 in place.
Inquiry Activity Reflection:
1. The connections that I see between Unit N,O,P, and Q so far are all related to the unit circle. In order to solve and understand most of them, you must fully understand and keep in mind the unit circle. Having memorized the unit circle is key.
2. If i had to describe trigonometry in THREE words, they would be difficult, challenging, and memorization. Trigonometry really requires a lot of practice and memorization of the unit circle. You can not solve the problems if you do not know the unit circle, formulas, sin, cos, tan, and so much more.
Monday, March 17, 2014
BQ#1: Unit P Concepts 2 and 4: Law of Sins and Area Formulas
2. Law of Sins: Why is SSA ambiguous?
It is ambiguous because sometimes the three parts that are given will one triangle, two triangles, or not not one triangle at all. Below is an example of a two triangle.
4. Area Formulas: How is the “area of an oblique” triangle derived?
It is derived from the triangle area formula= 1/2bh. In order to know the height of we have to make two triangles by drawing a line down the middle from angle B. We then label that line h because it is the height. With the given information above in the picture, we take the sin of A and equal it to Sin C. We multiply C to each side leaving us with CsinM<A=h. Next, plug in 1/2bh and we get A=1/2b(asinC). For a better understanding click the link below watch the video:
https://www.youtube.com/watch?v=XvIKUYBiAVY
It is ambiguous because sometimes the three parts that are given will one triangle, two triangles, or not not one triangle at all. Below is an example of a two triangle.
4. Area Formulas: How is the “area of an oblique” triangle derived?
It is derived from the triangle area formula= 1/2bh. In order to know the height of we have to make two triangles by drawing a line down the middle from angle B. We then label that line h because it is the height. With the given information above in the picture, we take the sin of A and equal it to Sin C. We multiply C to each side leaving us with CsinM<A=h. Next, plug in 1/2bh and we get A=1/2b(asinC). For a better understanding click the link below watch the video:
https://www.youtube.com/watch?v=XvIKUYBiAVY
Wednesday, March 5, 2014
WPP#12: Unit O Concept 10: Solving Elevation and Depression Problems
 |
| http://www.whenwegetthere.com/tourist_attraction_images/land_ tourist_attractions/mountain_climbing/mountain_climbing.jpg |
1B) Ana finally decides to wake up to catch up to Ricky and they both then climb to the top of the mountain which is 215 ft above ground level. They are so high above that they can see their tent from a 30 degree angle of depression. What is the horizontal distance above ground from the top of the mountain to the tent?
Tuesday, March 4, 2014
I/D#2: Unit O- How Can We Derive the Patterns for a Special Right Triangle?
INQUIRY ACTIVITY SUMMARY
1. 30-60-90 Triangle
This equilateral triangle has all sides equalling one (because given) and the angles equalling 60 degrees. We know that because all angles in a triangle sum up to 180, and since there are 3 angles you divide 180 by 3 giving you 60 for each angle. However, to get our 30-60-90 triangle, we must cut the triangle vertically in half, having the top 60 degrees become two 30 degree angles and the middle bottom of the triangle two 90 degree angles as seen below. As for the sides equalling one, since we cut the triangle in half, each triangle is going to have the bottom side equalling 1/2. To find the other sides, we use the Pythagorean theorem which is a^2+b^2=c^2. In this case were solving 1/2^2+b^2=c^2 which results in b= radical 3 over 2. To make it easier and not deal with fractions we multiply everything by 2 and add a variable, n, to represent any number, meaning the relationship is consistent. We then get a=2n , b=radical 3 over 3, and c= n.
2. 45-45-90 Triangle
Since we want a 45-45-90 triangle, we cut the square diagnolly in half. How do we know we got two 45 degree angles? Well, a square has all 90 degree angles and when we cut it diagonally in half, the two 90 degree angles split into two, meaning the 90 degree angle is divided by 2 as seen below. We are given that all sides equal one but since we don't not know one of the sides because we cut the square we use the Pythagorean theorem which is a^2+b^2=c^2. In this case were solving 1^2+1^2=c^2, giving us c=radical 2. We then add n to each side in which represents any number meaning the relationship is consistent.
INQUIRY ACTIVITY REFLECTION
1. Something i never noticed about a special right triangle is that there will always be two sides that are the same for example a 45-45-90 triangle a and b are the same and in a 30-60-90 triangle.
2. Being able to derive these patterns myself aids in my learning because it gives me a better understanding of how everything connects. If i every forget the rules i can simply derive them.
1. 30-60-90 Triangle
This equilateral triangle has all sides equalling one (because given) and the angles equalling 60 degrees. We know that because all angles in a triangle sum up to 180, and since there are 3 angles you divide 180 by 3 giving you 60 for each angle. However, to get our 30-60-90 triangle, we must cut the triangle vertically in half, having the top 60 degrees become two 30 degree angles and the middle bottom of the triangle two 90 degree angles as seen below. As for the sides equalling one, since we cut the triangle in half, each triangle is going to have the bottom side equalling 1/2. To find the other sides, we use the Pythagorean theorem which is a^2+b^2=c^2. In this case were solving 1/2^2+b^2=c^2 which results in b= radical 3 over 2. To make it easier and not deal with fractions we multiply everything by 2 and add a variable, n, to represent any number, meaning the relationship is consistent. We then get a=2n , b=radical 3 over 3, and c= n.
2. 45-45-90 Triangle
Since we want a 45-45-90 triangle, we cut the square diagnolly in half. How do we know we got two 45 degree angles? Well, a square has all 90 degree angles and when we cut it diagonally in half, the two 90 degree angles split into two, meaning the 90 degree angle is divided by 2 as seen below. We are given that all sides equal one but since we don't not know one of the sides because we cut the square we use the Pythagorean theorem which is a^2+b^2=c^2. In this case were solving 1^2+1^2=c^2, giving us c=radical 2. We then add n to each side in which represents any number meaning the relationship is consistent.
INQUIRY ACTIVITY REFLECTION
1. Something i never noticed about a special right triangle is that there will always be two sides that are the same for example a 45-45-90 triangle a and b are the same and in a 30-60-90 triangle.
2. Being able to derive these patterns myself aids in my learning because it gives me a better understanding of how everything connects. If i every forget the rules i can simply derive them.
Friday, February 28, 2014
I/D# 1: Unit N Concepts 7-9 : How Do Special Right Triangles and the Unit Circle Relate?
INQUIRY ACTIVITY SUMMARY
1. Describe a 30 degree Angle
I first labeled the triangle according to the Special Right Triangle Rules which is the hypotenuse 2x, the horizontal value x radical 3, and the vertical value x. I then had to simplify the three sides of the triangle fairly in a way such that the hypotenuse=1 so i divided each side by 2x (which is the hypotenuse) giving me: r=1, x=radical 3 over 2, and y= 1/2. I labeled the hypotenuse r, the horizontal value x, and the vertical value y. In order to draw a coordinate plane for each angle i first put the ordered pair (0,0) at the 30 degree corner, then since our x= radical 3 over 2, i knew my ordered pair for the 90 degree angle was (radical 3 over 2,0) because it didn't move up the y axis. For the 60 degree angle, i simply already knew that x=radical 3 over 2 and our y=1/2 so i put them as the ordered pair (radical 3 over 2, 1/2) since it moved x units to the right and y units up.
2. Describe a 45 Degree Angle
I first labeled the triangle according to Special Right Triangle Rules which is the hypotenuse x radical 2, the horizontal value x, and the vertical value x as well. In order to have the hypotenuse equal to one as i divided each side by the value of the hypotenuse which is x radical 2 resulting in as r=1, x=radical 2 over 2, y=radical 2 over 2. I labeled the hypotenuse r, the horizontal value x, and the vertical value y. To find the coordinate planes, i applied the same concept as i did for the 30 degree angle above. I put the ordered pair (0,0) at the 45 degree left corner, then since our x= radical 2 over 2, i knew my ordered pair for the 90 degree angle was (radical 2 over 2 over 2,0) because we didn't move up the y axis. For the other 45 degree angle, i simply already knew that x=radical 2 over 2 and our y=radical 2 over 2, so i put them as the ordered pair (radical 2 over 2, radical 2 over 2) because we moved x units to the right and y units up.
3. Describe a 60 degree Angle
I first labeled the triangle according to Special Right Triangle Rules which is the hypotenuse 2x, the horizontal value x, and the vertical value x radical 3. To have the hypotenuse equaling to one, i divided it by itself and the other sides as well having r=1, x=1/2, y=radical 3 over 2. I labeled the hypotenuse r, the horizontal value x, and the vertical value y.To find the coordinate planes, i applied the same concept as i did for the above angles. I put the ordered pair (0,0) at the 60 degree left corner, then since our x= 1/2 , i knew my ordered pair for the 90 degree angle was (radical 2 over 2 over 2,0) because we didn't move up the y axis and moved x units to the right. For the 30 degree angle, i simply already knew that x=1/2 and our y= radical 3 over 2, so i put them as the ordered pair (radical 2 over 2, radical 2 over 2) because we moved x units to the right and y units up.
4. This activity helped me derive the unit circle because it gave me the coordinates, points, and angles that are within the unit circle as seen below. I understood the foundation of it, allowing me to not only have to memorize numbers but know why those numbers exist. I thought it was important to do this activity because it gave me the basic comprehension of what a unit circle is.
5. The 30, 45, and 60 degree angles are within the first quadrant of the unit circle. The second quadrant is a reflection of the first, the third is a reflection of the second, and the fourth is a reflection of the third. In the first quadrant, all coordinates are positive, in the second quadrant, only the x value is negative, in the third quadrant both x and y are negative and in the fourth quadrant only the y is negative having that the first and third quadrant are positive and the second and fourth are negative. For a better understanding look below.
Inquiry Reflection Activity
1. The coolest thing I learned from this activity was how each quadrant is reflected with triangles.
2. This activity will help me in this unit because understanding and memozing the unit circle is a basic need to solve problems in all the concepts.
3. Something I never realized before about special right triangles and the unit circle is that the whole unit circle consists of many right right triangles that give it its coordinates.
1. Describe a 30 degree Angle
I first labeled the triangle according to the Special Right Triangle Rules which is the hypotenuse 2x, the horizontal value x radical 3, and the vertical value x. I then had to simplify the three sides of the triangle fairly in a way such that the hypotenuse=1 so i divided each side by 2x (which is the hypotenuse) giving me: r=1, x=radical 3 over 2, and y= 1/2. I labeled the hypotenuse r, the horizontal value x, and the vertical value y. In order to draw a coordinate plane for each angle i first put the ordered pair (0,0) at the 30 degree corner, then since our x= radical 3 over 2, i knew my ordered pair for the 90 degree angle was (radical 3 over 2,0) because it didn't move up the y axis. For the 60 degree angle, i simply already knew that x=radical 3 over 2 and our y=1/2 so i put them as the ordered pair (radical 3 over 2, 1/2) since it moved x units to the right and y units up.
2. Describe a 45 Degree Angle
I first labeled the triangle according to Special Right Triangle Rules which is the hypotenuse x radical 2, the horizontal value x, and the vertical value x as well. In order to have the hypotenuse equal to one as i divided each side by the value of the hypotenuse which is x radical 2 resulting in as r=1, x=radical 2 over 2, y=radical 2 over 2. I labeled the hypotenuse r, the horizontal value x, and the vertical value y. To find the coordinate planes, i applied the same concept as i did for the 30 degree angle above. I put the ordered pair (0,0) at the 45 degree left corner, then since our x= radical 2 over 2, i knew my ordered pair for the 90 degree angle was (radical 2 over 2 over 2,0) because we didn't move up the y axis. For the other 45 degree angle, i simply already knew that x=radical 2 over 2 and our y=radical 2 over 2, so i put them as the ordered pair (radical 2 over 2, radical 2 over 2) because we moved x units to the right and y units up.
3. Describe a 60 degree Angle
I first labeled the triangle according to Special Right Triangle Rules which is the hypotenuse 2x, the horizontal value x, and the vertical value x radical 3. To have the hypotenuse equaling to one, i divided it by itself and the other sides as well having r=1, x=1/2, y=radical 3 over 2. I labeled the hypotenuse r, the horizontal value x, and the vertical value y.To find the coordinate planes, i applied the same concept as i did for the above angles. I put the ordered pair (0,0) at the 60 degree left corner, then since our x= 1/2 , i knew my ordered pair for the 90 degree angle was (radical 2 over 2 over 2,0) because we didn't move up the y axis and moved x units to the right. For the 30 degree angle, i simply already knew that x=1/2 and our y= radical 3 over 2, so i put them as the ordered pair (radical 2 over 2, radical 2 over 2) because we moved x units to the right and y units up.
4. This activity helped me derive the unit circle because it gave me the coordinates, points, and angles that are within the unit circle as seen below. I understood the foundation of it, allowing me to not only have to memorize numbers but know why those numbers exist. I thought it was important to do this activity because it gave me the basic comprehension of what a unit circle is.
5. The 30, 45, and 60 degree angles are within the first quadrant of the unit circle. The second quadrant is a reflection of the first, the third is a reflection of the second, and the fourth is a reflection of the third. In the first quadrant, all coordinates are positive, in the second quadrant, only the x value is negative, in the third quadrant both x and y are negative and in the fourth quadrant only the y is negative having that the first and third quadrant are positive and the second and fourth are negative. For a better understanding look below.
Inquiry Reflection Activity
1. The coolest thing I learned from this activity was how each quadrant is reflected with triangles.
2. This activity will help me in this unit because understanding and memozing the unit circle is a basic need to solve problems in all the concepts.
3. Something I never realized before about special right triangles and the unit circle is that the whole unit circle consists of many right right triangles that give it its coordinates.
Tuesday, February 11, 2014
RWA#1:Unit M Concepts 4-6: Graphing and Identifying all Parts of an Ellipse
1) Definition
"The set of all points such that the sum of the distance from two points is a constant." (Crystal Kirch)
2)
| http://www.mesacc.edu/~marfv02121/readings/conics/conics-2.GIF |
The above equations show an ellipse in standard form also meaning both term terms are squared, added, and have different coefficients. In standard from we can find the vertex, by using the h and k, and we can find our a and b by taking the square root of the a and b in the standard form. a is the distance in units away from the center and the vertex and b is the distance in units from the center to the co vertices. you can also use b to find the co-vertices which are the endpoints of the minor axis. To find c you must use the equation a^2 -b^2=c^2. c is the distance in units from the center to the foci. the c will also be a part of the foci. The below pictures give a visual.
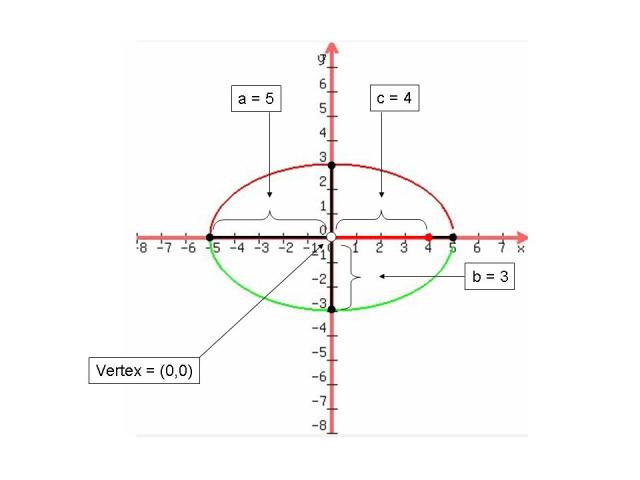
Horizontal
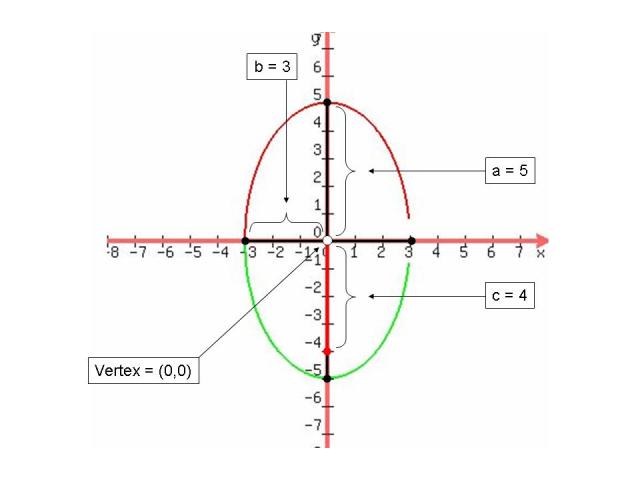
Vertical
The following parts to graph an ellipse are the: foci's, major axis, minor axis, and the eccentricity. The foci are spaced equally on each side of the center and they always lies on the major axis.The closer the foci is from the end point the skinnier the graph gets. To graph the foci you must plot the amount of c units to the right/left if x is squared but if y is squared then plot them up/down. identify whether the major axis is horizontal or vertical you must see if the bigger denominator in under the "y" squared or the "x" squared. If it is the bigger denominator is under the "x" squared term than it is horizontal and if its under the "y" squared term than it is vertical. The eccentricity of an ellipse (the measurement of how much a conic section varies from being a circle and for must be) must be greater than 0 but less than one. To find it you divide c and a. For more detailed instructions see: http://jwilson.coe.uga.edu/EMAT6680/Brown/6690/InstrUnit/DayFive.htm
For better instructions on how to graph an ellipse watch the video below.
4) Works cited
 |
| http://theo.x10hosting.com/examples/Ellipse/Ellipse6.jpg |
 |
| http://theo.x10hosting.com/examples/Ellipse/Ellipse7.jpg |
For better instructions on how to graph an ellipse watch the video below.
3) Real World Application
Our solar system is an example of an ellipse. You may think that most objects in space orbit in circles, however that is not the case. Although some do follow circular orbits most orbits are shaped like a stretched out circle. All of the planets in our solar system move along elliptical orbits having the sun as a foci. The orbits of the moon and satellites of the moon are also elliptical. (http://www.windows2universe.org/physical_science/physics/mechanics/orbit/ellipse.html)
4) Works cited
- http://www.mesacc.edu/~marfv02121/readings/conics/conics
- 2.GIFhttp://theo.x10hosting.com/examples/Ellipse/Ellipse6.jpg
- http://theo.x10hosting.com/examples/Ellipse/Ellipse7.jpg
- https://www.youtube.com/watch?v=5nxT6LQhXLM
- http://www.windows2universe.org/physical_science/physics/mechanics/orbit/ellipse.html
- http://jwilson.coe.uga.edu/EMAT6680/Brown/6690/InstrUnit/DayFive.htm
Subscribe to:
Posts (Atom)











